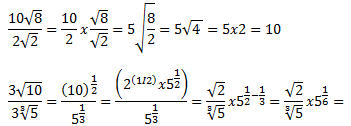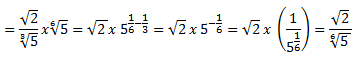A) Suma de radicales.
LA regla general es que solo podemos operar con radicales semejantes, vamos a diferenciarlos:
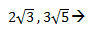No son semejantes, ya que tienen distintos coeficientes
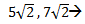Son semejantes, ya que poseen el mismo coeficiente, ese raíz de dos.
**Nota: El coeficiente debe ser el mismo tanto en número como en índice, es decir, no podríamos operar con un raíz cúbica y una raíz cuadrada.
B) Resta de radicales.
Si habéis entendido el apartado anterior, este os será fácil, ya que es lo mismo, pero restando, como si fuesen números normales, siempre respetando los coeficientes, por supuesto. Ejemplo:
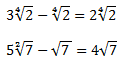
C) Multiplicación de radicales.
Como antes, para poder multiplicar, los radicales han de ser del mismo orden, es decir, semejantes.
Multiplicaremos los radicales y los números que los multiplican por separado. Ejemplo:
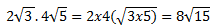
D) División de radicales.
Lo mismo que explicamos en la multiplicación pasa en la división, el proceso es exactamente el mismo, realizaremos dos divisiones por separado, las de los números enteros por un lado y las de los radicales por el otro, siempre teniendo en cuenta si son semejantes, esto quiere decir, que no podríamos “disminuir” una raíz cubica con una cuadrada. Ejemplo:
